パソコンでの閲覧では一部レイアウトが崩れる場合があります。スマートフォン・タブレットでご覧いただくことを推奨しております。
A4
2次関数
20
解答
のとき，最小値
| 取り組み結果 |
|---|
 |
 |
 |
のとき，
で，これを変形すると
を平方完成して
となる。
の係数が正であるから，
の最小値は
で，そのときの
の値は
である。
答えを求めて
答 
のとき，最小値
解答
| 取り組み結果 |
|---|
|
|
|
を変形すると
を平方完成して
となる。の係数が正であるから，の最小値は
である。よって，最小値が負になるのは
答えを求める式を立てて
のときで，これより
答えを求めて
答 
〔の別解〕
のの係数が正であるから，
のグラフは下に凸の放物線である。よって，の最小値が負になるのはのグラフが軸と異なる
点を共有するとき，すなわち次方程式
が異なるつの実数解をもつときである。よって
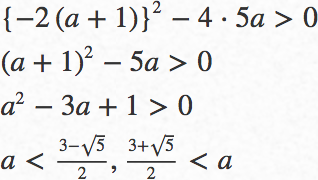
答えを求める式を立てて
答えを求めて
答 
解答
| 取り組み結果 |
|---|
|
|
|
より，
のグラフは，軸が直線
で，下に凸の放物線である。
より，
であるから，次のつの場合が考えられる。
(ⅰ) 
，すなわち
のとき
▲
のグラフが下に凸の放物線で，定義域に制限があるとき，その軸の位置によって，
が最小となる
の値が異なってくる。(ア)軸が区間の左外にある場合は区間の左端で，(イ)軸が区間内にあるときは軸の位置で，(ウ)軸が区間の右外にある場合は区間の右端で，はそれぞれ最小となる。本問の場合は(ア)の場合は起こらず，(イ)が(ⅰ)に，(ウ)が(ⅱ)にあたる。
におけるのグラフは上図のようになり，は
で最小となり，最小値は
(ⅰ)のときの場合分けと最小値を求めて
よって，最小値が
であることから
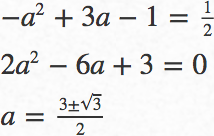
であるから，
が適する。
(ⅰ)のときの場合分けと答えに
(ⅱ) 
，すなわち
のとき
におけるのグラフは上図のようになり，は
で最小となり，最小値は
(ⅱ)のときの場合分けと最小値を求めて
よって，最小値がであることから
これは
に適している。
(ⅱ)のときの場合分けと答えを求めて
以上，(ⅰ)，(ⅱ)により，求める
の値は
答