パソコンでの閲覧では一部レイアウトが崩れる場合があります。スマートフォン・タブレットでご覧いただくことを推奨しております。

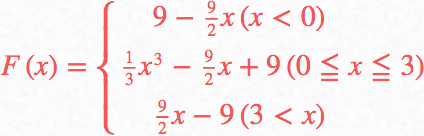

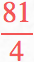

Z6
微分法・積分法(Ⅱ)

解答
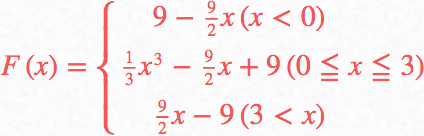
突破口
絶対値のついた関数の定積分を考えるときは,まず,積分区間における関数の符号を調べる。ここでは「![]() 」つまり
」つまり![]() についての積分であるから,
についての積分であるから,![]() の関数
の関数![]() の
の![]() における符号を考える。すると
における符号を考える。すると![]() を境にして
を境にして![]() の符号は変化するから,
の符号は変化するから,![]() と区間
と区間![]() の位置関係によって,場合分けをする必要があることがわかる。
の位置関係によって,場合分けをする必要があることがわかる。
〔解答〕
(ⅰ)![]() のとき
のとき
![]() において
において![]() であるから
であるから
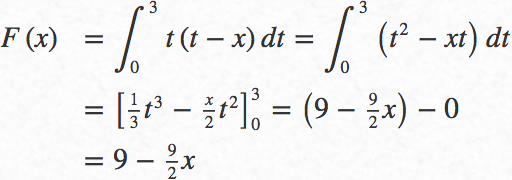
(ⅰ)のときの答えを求める式を立てて
(ⅰ)のときの答えを求めて
(ⅱ)![]() のとき
のとき
![]() において
において![]()
![]() において
において![]()
であるから
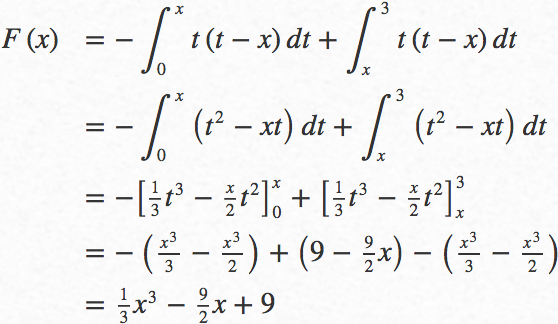
(ⅱ)のときの答えを求める式を立てて
(ⅱ)のときの答えを求めて
(ⅲ)![]() のとき
のとき
![]() において
において![]() であるから
であるから
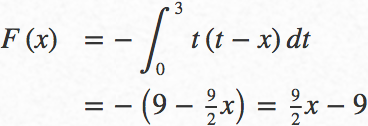
(ⅲ)のときの答えを求める式を立てて
(ⅲ)のときの答えを求めて
答 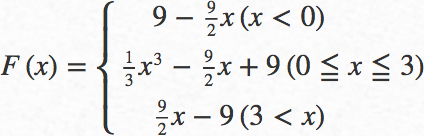

解答
突破口
まず,![]() のときの定積分
のときの定積分
![]() を
を と同様に考えて求める。面積を求めるときは,
と同様に考えて求める。面積を求めるときは,![]() における
における![]() と
と![]() の大小関係を調べて,定積分の式を作る。
の大小関係を調べて,定積分の式を作る。
〔解答〕
![]() で考えると
で考えると
区間![]() において
において![]()
であるから
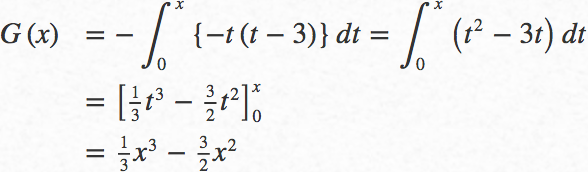
![]() での
での![]() を求める式を立てて
を求める式を立てて
![]() を求めて
を求めて
ここで,![]() において,常に
において,常に![]() であるから,求める部分の面積を
であるから,求める部分の面積を![]() とすると
とすると
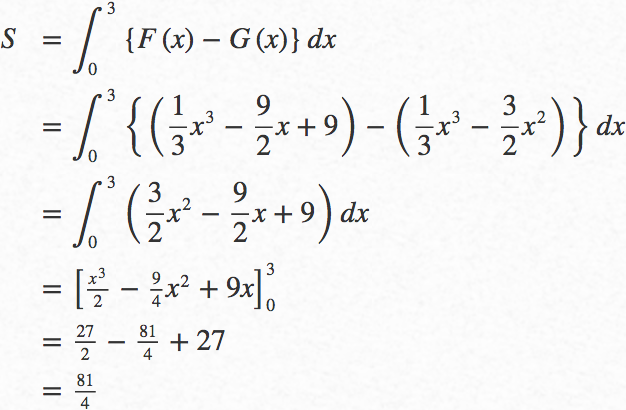

求める面積を定積分で表して
答えを求めて
答 ![]()